Today we will begin discussion about a significant concept, probability, which measures the likelihood of the occurrence of an event. This is the first part of the series, where you would be introduced to the core concept. So, let’s begin.
What is probability?
It is a measure of quantifying the likelihood that an event will occur and it is written as P(x).
Key concepts of probability
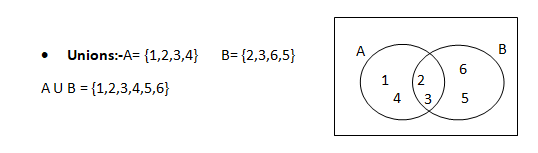
A union comprises of only unique values.
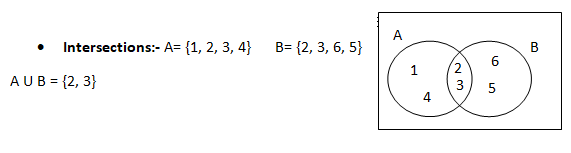
Intersection comprises of common values of the two sets
- Mutually Exclusive Events:- If the occurrence of one event preludes the occurrence of the other event(s), then it is called mutually exclusive event.
P(A∩B) = 0
- Independent Events:- If the occurrence or non-occurrence of an event does not have any effect on the occurrence or non-occurrence of other event(s), then it is called an independent event. For example drinking tea is independent of going for shopping.
- Collectively Exhaustive Events:– A set of collectively exhaustive events comprises of all possible elementary events for an experiment. Therefore, all sample spaces are collectively exhaustive sets.
- Complementary Events:– A complement of event A will be A` i.e. P(A`) = 1 ─ P(A)
Properties of probability
- Probabilities are non-negative values ranging between 0 & 1.
- Ω = 1 i.e. combined probability of sample is 1
- If A & B are two mutually exclusive events then P(A U B)= P(A) +P(B)
- Probability of not happening of an event is P(A)= 1 ─ P(A)
Rules of Counting the possibilities
- The mn counting rule:- When a customer has a set of combinations to choose from like two different engines, five different paint colors and three different interior packages , how will he calculate the total number of options available to him? The answer to the question is “ mn counting rule”. Simply multiply the given options, like in our case 2 * 5 * 3 will give us 30.This means the customer has 30 combinations to choose from when it comes to purchasing a car.
- Sampling from a population with replacement:- Suppose that you roll a dice three times i.e. the number of trials is 3, now if we want to check how many combinations are possible in this particular experiment we use Nn = 63 = 216
- Sampling from a population without replacement:- When the sample space shrinks after each trial then you use the following formula :-

Conclusion
There is a video covering the same concept attached down the blog, go through it to be more clear about this.
So, with this we wrap up our discussion on the concept of probability. If you want more informative blogs on Data Science training, then follow the Dexlab Analytics blog. Dexlab Analytics provides machine learning certification courses in gurgaon as well.
.
data science, Data Science Certification, Data Science Classes, Data Science Courses, data science online learning, Data Science training, Data Science training institute, Machine Learning, Machine Learning Certification, Machine Learning course, Machine Learning course in Gurgaon, Machine Learning course online, Machine Learning Courses, Machine Learning Training

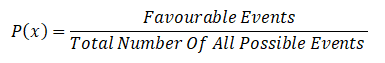
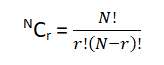
Comments are closed here.