Estimator Procedure under Simple Random Sampling: EXPLAINED

In continuation with the previous introductory blog on sampling: An ABC Guide to Sampling Theory, we will take a closer look into the concept of the estimator procedure under Simple Random Sampling with the help of mathematical examples. It will help us understand the underlying phenomenon, the manner to be precise in which the estimator function of sampling works.

Simple random sampling (SRS) is a method of selecting a sample comprising ‘n’ number of sampling units out of the population of ‘N’ number of sampling units such that every sampling unit has an equal chance of being chosen.

The Estimator Procedure under Simple Random Sampling

The process of selection of a sample under SRS (Simple Random Sampling) is random. This means, each number of the population has an equal probability of getting selected, which makes each of the observation identical and independently distributed.

The statistic chosen by the investigation of estimation of random samples need to satisfy a set of certain properties given below:

1. Unbiasedness
2. Consistency
3. Sufficiency
4. Efficiency

As a matter of fact, investigation is always about coming up with an idea regarding the population parameters based on the sample observations. The best part would be to formulate an unbiased, consistent estimator, which is also efficient. Normally, a sample mean for a set of sample observations is considered to be a very desirable estimator to form ideas about population parameters.

In detail, let’s examine the relevance of each of the properties of an estimator:

Unbiasedness of an estimator

Take a look at the below examples to understand the very idea of unbiasedness.

Example 1:

Answer:-

According to the problem, we have

Adding (1) & (2), we get,

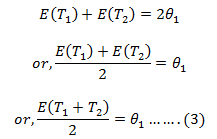
So, from (3), we get:-

 is called an unbiased estimators for .

Now, subtracting (2) & (1), we get –

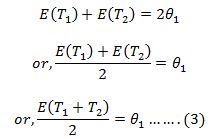
Example 2:

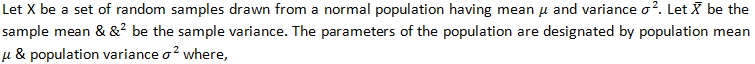
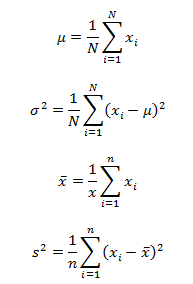
Assume that an investigator draws a sample from this population using SRSWR. Then show that the sample mean is an unbiased estimator for the population mean.

Now, by specification we have:-

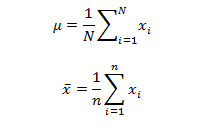
We are redefined to show that:-

L.H.S  :

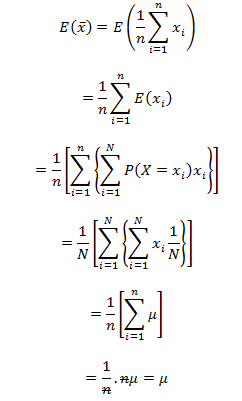
DexLab Analytics Presents #BigDataIngestion

Data sampling is the key to business analytics and data science. On that note, DexLab Analytics offers state of the art Data Science Certification for all data enthusiasts. Recently, they have organized a new admission drive #BigDataIngestion offering exclusive 10% off on in-demand courses, including big data, machine learning and data science courses.

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.