The Almighty Central Limit Theorem

The Central Limit Theorem (CLT) is perhaps one of the most important results in all of the statistics. In this blog, we will take a glance at why CLT is so special and how it works out in practice. Intuitive examples will be used to explain the underlying concepts of CLT.

First, let us take a look at why CLT is so significant. Firstly, CLT affords us the flexibility of not knowing the underlying distribution of any data set provided if the sample is large enough. Secondly, it enables us to make “Large sample inference” about the population parameters such as its mean and standard deviation.

The obvious question anybody would be asking themselves is why it is useful not to know the underlying distribution of a given data set?

To put it simply in real life, often times than not the population size of anything will be unknown. Population size here refers to the entire collection of something, like the exact number of cars in Gurgaon, NCR at any given day. It would be very cumbersome and expensive to get a true estimate of the population size. If the population size is unknown its underlying distribution will be known too and so will be its standard deviation. Here, CLT is used to approximate the underlying unknown distribution to a normal distribution. In a nutshell, we don’t have to worry about knowing the size of the population or its distribution. If the sample sizes are large enough, i.e. – we have a lot of observed data, it takes the shape of a symmetric bell-shaped curve. 

Now let’s talk about what we mean by “Large sample inference”. Imagine slicing up the data into ‘n’ number of samples as below:

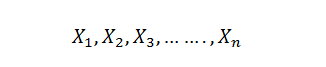
Now, each of these samples will have a mean of their own.

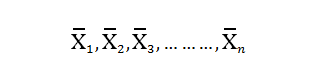
Therefore, effectively the mean of each sample is a random variable which follows the below distribution:

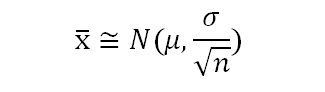
Imagine, plotting each of the sample mean on a line plot, and as “n”, i.e. the number of samples goes to infinity or a large number the distribution takes a perfect bell-shaped curve, i.e – it tends to a normal distribution.

Large sample inferences could be drawn about the population from the above distribution of x̅. Say, if you’d like to know the probability that any given sample mean will not exceed quantity or limit.

The Central Limit Theorem has vast application in statistics which makes analyzing very large quantities easy through a large enough sample. Some of these we will meet in the subsequent blogs.

Try this for yourself: Imagine the average number of cars transiting from Gurgaon in any given week is normally distributed with the following parameter . A study was conducted which observed weekly car transition through Gurgaon for 4 weeks. What is the probability that in the 5^th week number of cars transiting through Gurgaon will not exceed 113,000?

If you liked this blog, then do please leave a comment or suggestions below.

About the Author: Nish Lau Bakshi is a professional data scientist with an actuarial background and a passion to use the power of statistics to tackle various pressing, daily life problems.

About the Institute: DexLab Analytics is a premier data analytics training institute headquartered in Gurgaon. The expert consultants working here craft the most industry-relevant courses for interested candidates. Our technology-driven classrooms enhance the learning experience.

Interested in a career in Data Analyst?

To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.

To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.