
Regression analysis is extensively used in business applications. It’s one of the most integral statistical techniques that help in estimating the direction and strength between two or more (financial) variables – thus determining a company’s sales and profits over the past few years.
In this blog, we have explained how a regression line is the best fit for a given PRF if the parameters are all OLS estimations.
The OLS estimators for a given regression line has been obtained as: a = y ̅ – bx ̅ and b = (Cov(x,y))/(v(x)). The regression line on the basis of these OLS estimate has been given as: Y ̂_ i-Y ̅ = b(x_i-x ̅ )….. (1)
The regression line (1) constructed above is a function of the least square i.e. the parameters of the regression equation have been selected so that the residual sum of squares is minimized. Thus, the estimators ‘a’ & ‘b’ explains the population parameters, the best relative to any other parameters. Given, the linearity of the parameters, these estimators share the minimum variations with the population parameters, i.e. they explain the maximum variations in the model, in relation to the population parameters, as compared to any other estimators, in a class of unbiased estimators.
Thus, the regression line would be the ‘best fit’ for a given PRF. If ‘a’ & ‘b’ are best linear unbiased estimators for respectively. Thus, to show ‘best fit’, we need to prove:

To ‘b’ is Best unbiased estimator for :-
From the OLS estimation; we have ‘b’ as:
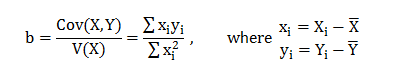
![]()
i.e.b is a linear combination of w’is & y’is.
Hence; ‘b’ is a linear estimator for β. Therefore, the regression line would be linear in parameters as far as ‘b’ is concerned.
Now,
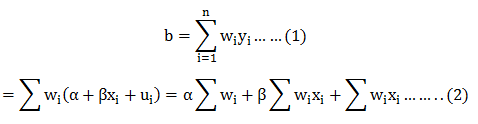
![]()
Let us test for the prevalence of this conditions:
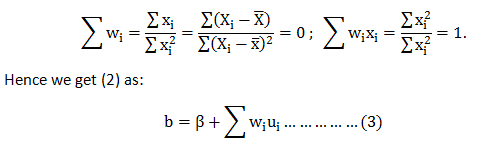
For unbiasedness, we must have :- E(b)=β. To test this, we take expectation on both sides of (3) & get:
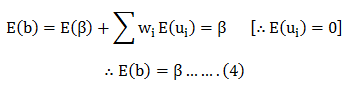
From (1) & (4) we can say that ‘b’ is a linear unbiased estimator for β.
To check whether ‘b’ is the best estimator or not we need to check whether it has the minimum variance in a class of linear unbiased estimator.
Thus, we need to calculate the variance for ‘b’ & show that it is the minimum in a class of unbiased estimations. But, first, we need to calculate the variance for ‘b’.
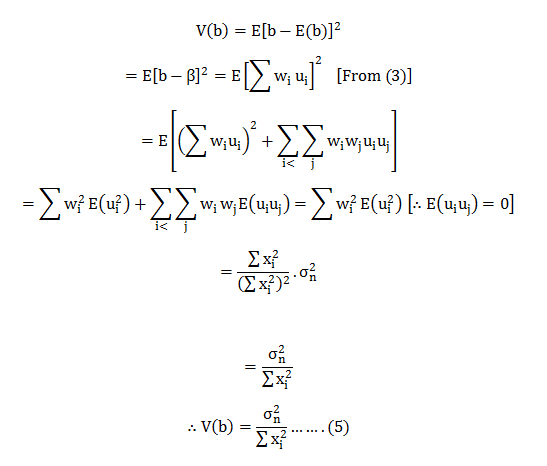
Now; we need to construct another linear unbiased estimator and find its variance.
Let another estimator be: b^*=∑ci yi….(6) For unbiasedness ∑ci =0,∑cixi =1.
Now; from (6) we get:
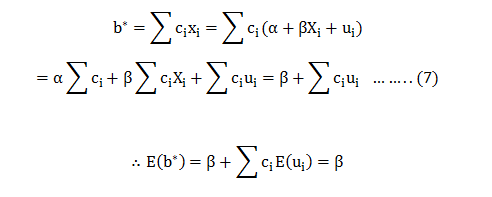
∴b* is an unbiased estimator for Now; the variance for can be calculated as:-
Now;
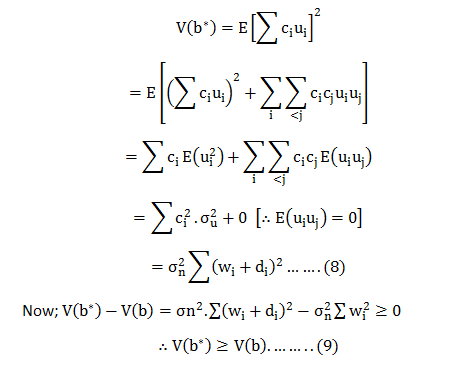
Hence; from (9) we can say V(b) is the least among a class of unbiasedness estimators.
Therefore, ‘b’ is the best linear unbiased estimator for in a class of linear unbiased estimators.
To prove ‘a’ is the best linear unbiased estimator for α:-
Form the OLS estimation we have ‘a’ as:-
![]()
Here; ‘b’ is a function of Y and Y is a linear function of X(orUi).
‘a’ is also a linear function of Y. i.e. has linearity.
There, ‘a’ is a linear estimator for ……. (11)
Now, for ‘a’ to be an unbiased estimator; we must have From (10) we have:-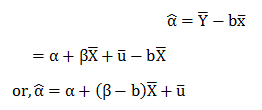
Taking expectations on both sides of the equation; we get:
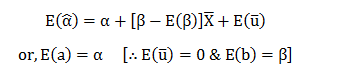
Therefore, ‘a’ is an unbiased estimator for ……… (12)
From (11) & (12) ‘a’ is a linear unbiased estimator for
Now, if ‘a’ is to be the best estimator for then is most have the minimum variance. Thus; we first need to calculate the variance of ‘a’.
Now,
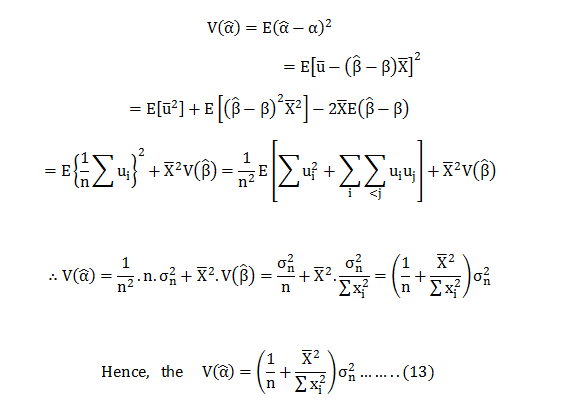
Now; let us consider an estimator in the class of linear unbiased estimator.
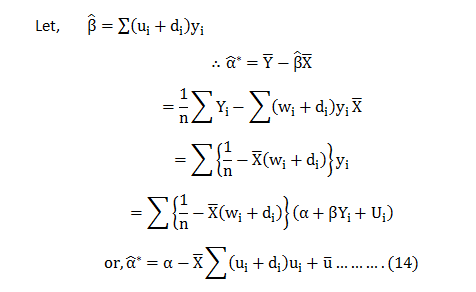 Further we know,
Further we know,
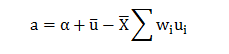
Now;
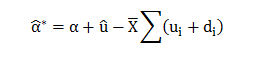
Hence;
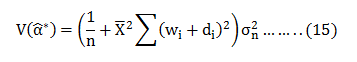
Now;
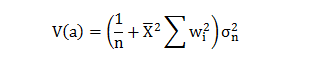
Therefore;
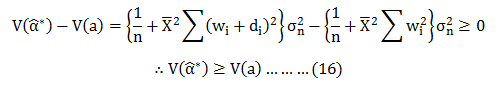
Hence; from (16) we can say that is the Min Variance Unbiased estimator in a class of unbiased estimator.
Hence; we can now safely conclude that a regression line composed of OLS estimators is the ‘best fit’ line for a given PRF, compared to any other estimator.
Thus, the best-fit regression line can be depicted as
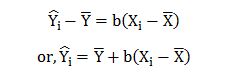
![]()
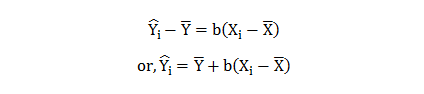 Thus, a regression line is the best fit for a given PRF if the estimators are OLS.
Thus, a regression line is the best fit for a given PRF if the estimators are OLS.
End Notes
The beauty and efficiency of Regression method of forecasting never fail to amaze us. The way it crunches the data to help make better decisions and improve the current position of the business is incredible. If you are interested in the same, follow us at DexLab Analytics. A continues blog series on regression model and analysis is upcoming. Watch this space for more.
DexLab Analytics offers premium data science courses in Gurgaon crafted by the experts. After thorough research, each course is prepared keeping student’s needs and industry demands in mind. You can check out our course offerings here.
Interested in a career in Data Analyst?
To learn more about Data Analyst with Advanced excel course – Enrol Now.
To learn more about Data Analyst with R Course – Enrol Now.
To learn more about Big Data Course – Enrol Now.To learn more about Machine Learning Using Python and Spark – Enrol Now.
To learn more about Data Analyst with SAS Course – Enrol Now.
To learn more about Data Analyst with Apache Spark Course – Enrol Now.
To learn more about Data Analyst with Market Risk Analytics and Modelling Course – Enrol Now.
analytics course in delhi, analytics courses, analytics courses in delhi ncr, analytics training institute, Data analyst certification, Data analyst course, data analyst course in delhi, data analyst institute, Data analyst training institute, data analytics, data analytics certification courses, data science, Data Science Certification, Data Science Classes, Data Science Courses, Data Science training, Data Science training institute

Comments are closed here.